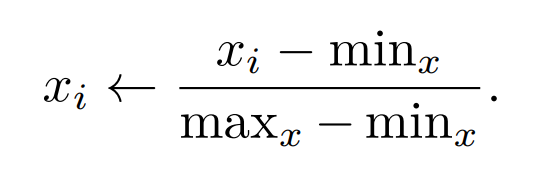Machine learning - různá témata (FIT)

Rozdělení dat pro trénování, validaci a testování

• data si chci rozdělit na 3 skupiny
  • trénovací (největší skupina) - data použitá k trénování modelu, odhadování parametrů, tuningu apod.
  • validační - tato data nejsou použita k trénování, ale k ověřování různých verzí natrénovaného modelu
    • na těchto datech se měří chyba modelu a zároveň se ladí hyperparametry modelů
    • pomocí těchto dat také vybíráme nejlepší model (z různých tříd - stromy, kNN atd.)
  • testovací - tato data dosud ležela ladem a poslouží k jednorázovému ověření chování modelu pro neznámá data
    • na těchto datech se měří kvalita modelu
  • data by se měla vybrat náhodně (v sklearn je na to metoda)
  • poměrově by to mělo být:
    • 20 % testovací
    • 20 % ze zbytku validační
    • a zbytek trénovací (tam chci tu největší skupinu)
• nominální příznaky - kategorické (= nemají číselný význam a je jich konečné množství) příznaky, které nemají žádné přirozené uspořádání (např. místo narození, název, pohlaví)
• ordinální příznaky - také kategorické, ale mezi jednotlivými hodnotami je uspořádání (např. vzdělání - žádné < základní < s maturitou < vysokoškolské)
• spojité příznaky - jsou kvantitativní a nemají “konečný počet hodnot”
  • např. věk, cena, teplota apod.
• edit:
  • místo statického rozdělování na trénovací a validační data existuje lepší přístup - křížová validace (testovací data se musí “mechanicky” oddělit, to jinak nejde)
  • používá se např. cross_val_score
    • rozdělí si trénovací data na stejně velké skupiny (např. 5 skupin, 4 trénovací a 1 validační) a postupně natrénuje daný model trénovacími daty a vyzkouší model na validačních datech - z toho mu vyjde nějaké skóre
    • výstupem je průměr přes všechny různý skóre, tím pádem je daný model více robustní - protože nespoléhá tolik na náhodu při volbě validačních dat
  • pozor - pak po výběru konkrétních hyperparametrů podle křížové validace je dobré model finálně znovu natrénovat na VŠECH trénovacích datech, abychom měli co nejvíce dat pro trénování (s vybranými konkrétními hyperparametry)
  • na druhou stranu je křížová validace na velkém množství dat výpočetně hodně náročná, tak se používá hlavně, když těch dat není k dispozici tolik

Příprava dat

• problémy s daty mohou být různé (viz Jak dobře analyzovat data - sekce čištění dat)
• chybějící číselné hodnoty se dají nahradit průměrem (mean(), pomocí SimpleImputer)
• chybějící kategorické hodnoty se dají nahradit modusem (nejčastější hodnota, také se používá SimpleImputer)
• u přípravy dat řešíme také postup u nečíselných hodnot (protože nějaké modely akceptují pouze číselné hodnoty), dělíme je na (vysvětlení výše v Rozdělení dat pro trénování, validaci a testování):
  • ordinální
    • zavedeme pro ně nový datový typ “category” s definovaným pořadím a “ordered=True”
      • qual_category = pd.api.types.CategoricalDtype(categories=['Po', 'Fa', 'TA', 'Gd', 'Ex'], ordered=True)
      • a pak data[col] = data[col].astype(temp_category)
  • nominální
    • ty nejsou nijak seřazené, ale stejně je potřeba jim přiřadit kódy (pozor, kódy v trénovacích, validačních a testovacích datech musí sedět)
    • a zároveň je potřeba vzít v potaz pouze kategorie, které se vyskytují pouze v trénovacích datech (protože validační a trénovací data vlastně ten model ještě nikdy “neviděl”)
    • temp_category = pd.api.types.CategoricalDtype(categories=Xtrain[col].dropna().unique(), ordered=False)
      • jako kategorie vložím všechny možnosti z konkrétního col u TRÉNOVACÍCH dat (nechci duplicity a nechci mít NaN jako kategorii)
      • u validačních a testovacích dat se pak u kategorií které se neobjevily v trénovacích datech objeví NaN (s tím se pak pracuje dále - nahradí se -1, nebo modusem)

Ladění hyperparametrů

• používá se ParameterGrid pro různé možnosti parametrů
  • musím pak manuálně loopovat přes všechny parametry, ale dává mi to větší svobodu
• používá se GridSearchCV pro různé možnosti parametrů + rovnou křížová validace
• je potřeba dát pozor na overfitting - ne vždy je více možností parametrů ta správná cesta (může vést k většímu zachycení šumu)
• pro křížovou validaci lze použít: cross_val_score

Evaluace

• po natrénování a výběru finálního modelu je potřeba ještě zjistit, jak se model chová na nových datech (aka datech, která ještě neviděl - NE trénovací, NE validační)
• říká se tomu generalizace a evaluace toho modelu nám řekne, jak dobře je model schopný generalizovat a správně predikovat na nových datech
• pro regresi:
  • máme více ztrátových funkcí, které počítají míru “nepřesnosti” predikcí daného modelu - pak se často vypočítá průměr přes všechny “nepřesnosti”
    • jak moc se predikované hodnoty modelem liší od skutečných hodnot
    • cílem trénování je takovou funkci minimalizovat
  • nejčastěji se používá MSE (mean squared error) - penalizace velkých odchylek a odlehlých hodnot
  • root mean squared error - nelineárně přeškálované MSE
  • RMSLE - root mean squared logarithmic error - pro relativní odchylky (pro malé hodnoty řeší i malé odchylky a pro velké hodnoty pouze ty velké odchylky)
  • MAE - mean absolute error, používá abs. hodnotu, méně citlivá na odlehlé hodnoty než MSE
  • $R^2$ - koeficient determinace

Confusion matrix

• neboli matice záměn se používá k bližší evaluaci modelů - konkrétně klasifikačních
• při evaluaci klasifikačního modelu získáme skóre “přesnosti”, kolik procentuelně model předpověděl správných tříd (je to klasifikace)
• pro bližší prozkoumání se používá confusion matrix, která (při binární klasifikaci) rozdělí výsledky do 4 kategorií
  • TP = true positive, počet správně klasifikovaných do třídy 1
  • FP = false positive (počet nesprávně klasifikovaných do třídy 1)
  • FN = false negative (počet nesprávně klasifikovaných do třídy 0)
  • TN = true negative, počet správně klasifikovaných do třídy 0
• z těchto 4 čísel se dá počítat
  • accuracy - poměr správně klasifikovaných tříd
    • tj (TP+TN)/all samples
  • precision - kolik z predikovaných pozitivních je skutečně pozitivních?
    • jak “přesně” jsem predikoval TP?
    • TP / (TP + FP)
  • recall - kolik ze skutečně pozitivních je správně predikováno
    • kolik ze skutečných pozitivních případů model správně zachytil?
    • TP / (TP + FN)
  • F1 skóre - jedná se o harmonický průměr mezi precision a recall
    • hodí se hlavně tehdy, když máme hodně nevyvážené třídy (98 % zdravých a 2 % nemocných) - tady pokud měřím pouze accuracy a model všechny označí jako zdravé a nikoho jako nemocného, tak stejně mám 98 % accuracy a to je zavádějící
      • precision bude také vysoká, ale recall bude 0 → to se právě projeví i na tom F1 skóre
• pro vícetřídovou klasifikaci se jenom jedná o $nXn$ matici

ROC křivka

• = Receiver Operating Characteristic curve
• je to další metoda evaluace modelu (dívám se, jak se daný model chová)
  • pro klasifikační modely
• konkrétně se řeší tzv. rozhodovací práh (threshold), kdy se model rozhodne, jestli bude klasifikovat 0 či 1 pro konkrétní příznaky
• finální predikce v (např. rozhodovacím stromu či kNN) vznikne jako:
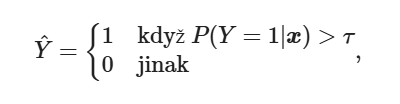
  • $x$ je vektor konkrétních příznaků, $\tau$ je daný threshold (často je to 0.5)
  • z natrénovaného modelu jsem schopen získat konkrétní pravděpodobnosti pro konkrétní hodnoty příznaků z Xtest (ala příznaky z testování) a $\tau$ rozhodne, jestli danou pravděpodobnost bude model klasifikovat jako 0 či 1
• 
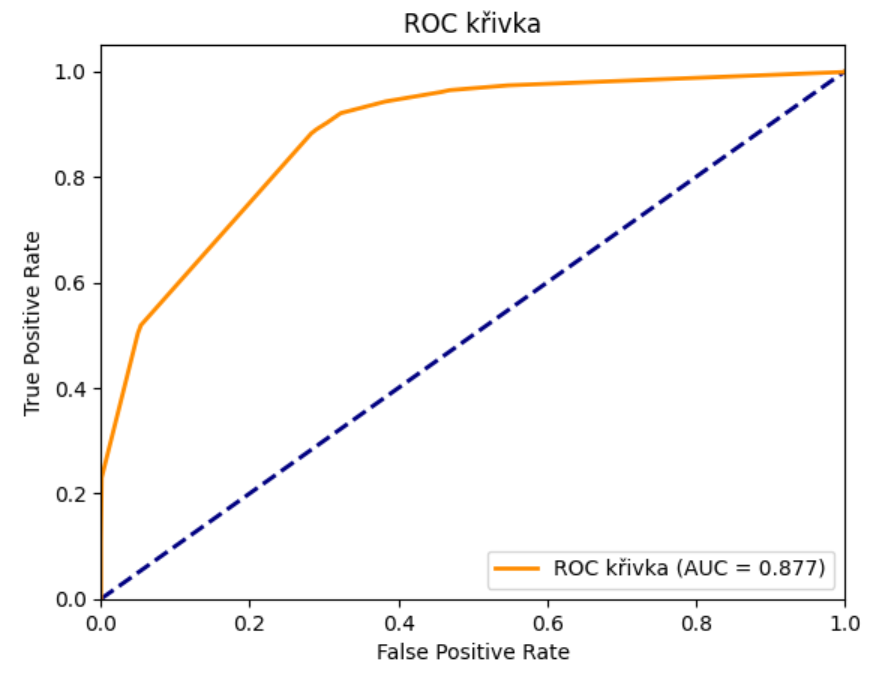
  • body na křivce udávají jednotlivé hodnoty thresholdu
    • v bodě (0,0) je threshold na hodnotě 1 (nic není positive, tj. TPR a FPR jsou obě na nue)
    • co snižuju threshold, tak se mi více a více pravděpodobností padá do positive (jak true positives, tak false positives)
    • a v bode (1,1) zase threshold pouští úplně všechno jako jedna
    • cílem je najít ten “sweet spot”, kde jsou maximalizovány TPR and minimalizovány FPR
  • zkoušíme jednotlivé hodnoty thresholdu, pro ty pak vypočítáme FPR a TPR a vznikne mi bod na křivce
    • FPR = FP / (FP +TN), FP vlastně “měl být false/negative”
      • “How often did I falsely raise the alarm?”
    • TPR = TP / (TP + FN), FN vlastně “měl být true/positive”
  • cílem je, aby se křivka co nejvíce “vypínala” do levého horního rohu (maximalizace TPR a minimalizace FPR), to kvantifikuje AUC (Area Under Curve)
    • 1 = dokonalý klasifikátor, 0.5 = náhodný klasifikátor, >0.5 = horší než náhoda (model dělá opačnou věc než kterou chceme)
    • velkou výhodou je to, že pro kvantifikování AUC (a tedy pro porovnávání modelů) nepotřebujeme pro každý z nich stanovovat konkrétní decision threshold (stačí nám výstupní pravděpodobnosti z modelu)
  • modrá čára je náhodný model, ukazuje, jak by ROC křivka vypadala u naprosto náhodného modelu
  • funkce model.predict_proba() - dostaneme pravděpodobnosti pro jednotlivé testovací příznaky
  • narozdíl od např. Profit curve nám umožňuje srovnávat modely aniž bychom museli mít definované cost-benefit matrix apod.

Rozhodovací stromy

• slouží jak pro regresi, tak i pro klasifikaci
• výhody:
  • poradí si s kategorickými (nominální, ordinální příznaky) i spojitými příznaky
  • poradí si s chybějícími hodnotami
  • srozumitelné, učení je rychlé
  • dobře interpretovatelné
• nevýhody:
  • malá změna v trénovacích datech může znamenat velkou změnu ve struktuře stromu
  • většinou se dělají pouze binární stromy (tedy, které se na jednom místě rozhodují pouze mezi dvěma “směry”)
  • najít optimální strom je NP-úplný problém
  • je snadné rozhodovací stromy přeučit (je to hodně flexibilní přístup)
• v praxi se používá CART = classification and regression trees

kNN

• k nejbližších sousedů, jedná se o supervizované učení
• samotná data už jsou “natrénovaná”
  • narozdíl od Rozhodovací stromy je trénování kNN modelu rychlé (je ihned) a predikování je pomalé - je totiž potřeba zjistit vzdálenost bodu, který chci predikovat od všech stávajících dat a pak predikovat hodnotu/kategorii na základě hodnot k nejbližších sousedů
    • aby nebylo nutné procházet všechny body, tak se data vhodně indexují
    • pak se rychlost tvorby modelu (tj. indexování dat) vyvažuje s rychlostí predikce (která je díky indexu rychlejší)
  • pro spojité veličiny (regrese) se používá průměr kNN
  • pro diskrétní veličiny (klasifikace) se používá nejčastější hodnota mezi kNN
• důležitá je vzdálenostní metrika
  • nejčastěji se používají Minkovského vzdálenosti (tj. $L_p$ vzdálenosti)
  • $L_1$ je Manhattanská, $L_2$ je Euklidovská
• kNN je možné snadno přeučit (overfitting), míru přeučení snížíme tím, že zvýšíme hyperparametr $k$
• další hyperparametry
  • weights - váhy jednotlivých bodů, často se používají pro zvýraznění důležitosti bližších sousedů (tj. klesají se vzdáleností)
  • míra vzdálenosti - Euklidovská, Manhattanská atd.
• vhodná je Normalizace dat před použitím kNN

Normalizace

• zvlášť pro kNN je vhodné data normalizovat (kNN je citlivé na přípravu dat)
  • proč?
    • různé rozsahy číselných hodnot u různých příznaků jsou různě interpretované
    • např. u datasetu s cenou domů se cena domu zvýší více přidáním 1 pokoje než přidáním $1m^2$ bazénu (a přitom z hlediska kNN je to 1 jako 1)
• existuje několik přístupů k normalizaci - žádný není nejlepší a všespásný
  • jednodušší lineární normalizace:
    • min-max normalizace: vezme se min a max hodnota u daného příznaku a ty se “namapují” na 0 a 1 a všechny hodnoty mezi nimi se přeškálují na interval (0,1)
      • 
    • standardizace: využívá se standardní rozdělení, výběrový průměr a výběrový rozptyl
      • 
• pozor! nechci normalizovat datový typ “bool”, ten je taky číselný, ale nedává smysl ho normalizovat
• pozor! fitování scaleru chci provádět pouze na trénovacích (nikoliv na validačních) datech, pak by validační chyba nebyla objektivní
  • resp. je potřeba data rozdělit před napočítáním Scaleru (např. MinMaxScaler nebo StandardScaler) pouze s použitím trénovacích dat
  • validační (a pak testovací) data pak přeškáluju také, ale s použitím napočítaného Scaleru z trénovacích dat
    • tato situace odpovídá realitě (budoucí data ještě nemám k dispozici) a pokud bych škáloval i podle validačních (a nedejbože testovacích), tak bych vlastně “viděl do budoucnosti” a dostal bych nerealisticky optimistické výsledky

Prokletí dimenzionality

• pozor na to, že se zvyšující se dimenzí (tj. počtem vstupních příznaků) se od sebe data vzájemně vzdalují
  • když se pak používají klasické metriky pro určení vzdálenosti, tak s rostoucí dimenzí se zmenšují rozdíly mezi blízkými a vzdálenými body
• jinými slovy: hustota trénovacích bodů s rostoucí dimenzí klesá
• pro redukci dimenzionality existují více přístupů a technik - jedná se o důležitou součástí zpracování dat pro efektivní machine learning

Lineární regrese

• problémy:
  • problémem je, pokud jsou nějaké sloupce lineárně závislé (to je problém kolinearity), nebo skoro lineárně závislé
    • pak je model lineární regrese špatně namodelovaný a pro malé změny v trénovacích datech se může dostat na velké změny v koeficientech + to zvyšuje varianci modelu (tj. také není tolik spolehlivý) → generalizuje špatně
    • řešením je snížení počtu příznaků které tvoří lineární závislost
    • typicky se provádí tzv. regularizace, kdy se přidává tzv. regularizační člen, který kolinearitu odstraní nebo alespoň zmírní (Hřebenová regrese)

Hřebenová regrese

• způsob, jak u Lineární regrese zmírnit příznaky kolinearity, zlepšit stabilitu a schopnost generalizovat
• jinak řečeno: $L_2$ regularizace
• do ztrátové funkce (měřící přesnost modelu, reziduální součet čtverců) přidává další (penalizační člen)
  • 
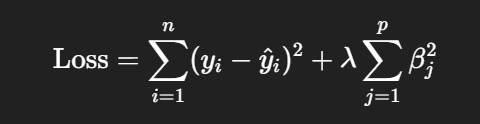
  • jehož cílem je penalizovat “moc velké koeficienty” a tím efektivně zabraňovat tomu, aby některé koeficienty “ulítly” do extrémních hodnot (v minimalizaci se bude cílit na vektory, které mají malé složky/koeficienty)
    • celá tahle funkce se minimalizuje, takže moc velké vektory (“ulítlé” vektory) se penalizují
    • celý model je pak stabilnější a redukuje se přeučení (overfitting) při kolinearitě nebo více redundantních prediktorů (které např. udávají tu stejnou hodnotu v jiných jednotkách - model je pak zmatený, které hodnoty má použít)
  • $\lambda =0:$ je normální lineární regrese
  • $\lambda >0:$ je regularizovaný reziduální součet čtverců

Další postup

• bias-variance trade-off
• bázové funkce - jak fungují a jak ovlivňují model