KOP 9. lecture

Simulated Evolution (genetic algorithms)

• based on the “survival of the fittest” from Darwin
• based on massive parallelism
  • it’s a way to avoid getting stuck in a local optimum
  • different parts of the state space are explored simultaneously
• it’s an iterative method - iterating generations
• crossover operation combines properties from two individuals
  • this is the main operation
  • 2 good individuals make even better individual
  • 2 bad individuals make even worse individual
    • selection operation is needed to eliminate the “bad” combinations
• genetic algorithms are solving ONLY optimization combinatorial problems (like Simulated annealing - KOP 8. lecture)

Terminology

• configuration is something abstract - it defines the form, how the individuals are encoded
• representation of configuration (configuration variables) is the actual encoding of the abstract configuration (actual values)
  • for standard genetics algorithms the configuration is often a vector of variables
    • binary string (011101001)
    • permutation (ordered list) - (1,2,5,8,7,5)
  • for each “gene” is important:
    • it’s value
    • it’s position in the vector
• diversity of a population
  • = measures, how much do the individuals (states) in the population differ
  • big diversity = a lot of state space parts are explored simultaneously (more parts of the state are changing)
  • small diversity = just a small part of an individual is explored/changing (the rest of the individuals’ states are the same) ⇒ degeneration of population

Genetic algorithms

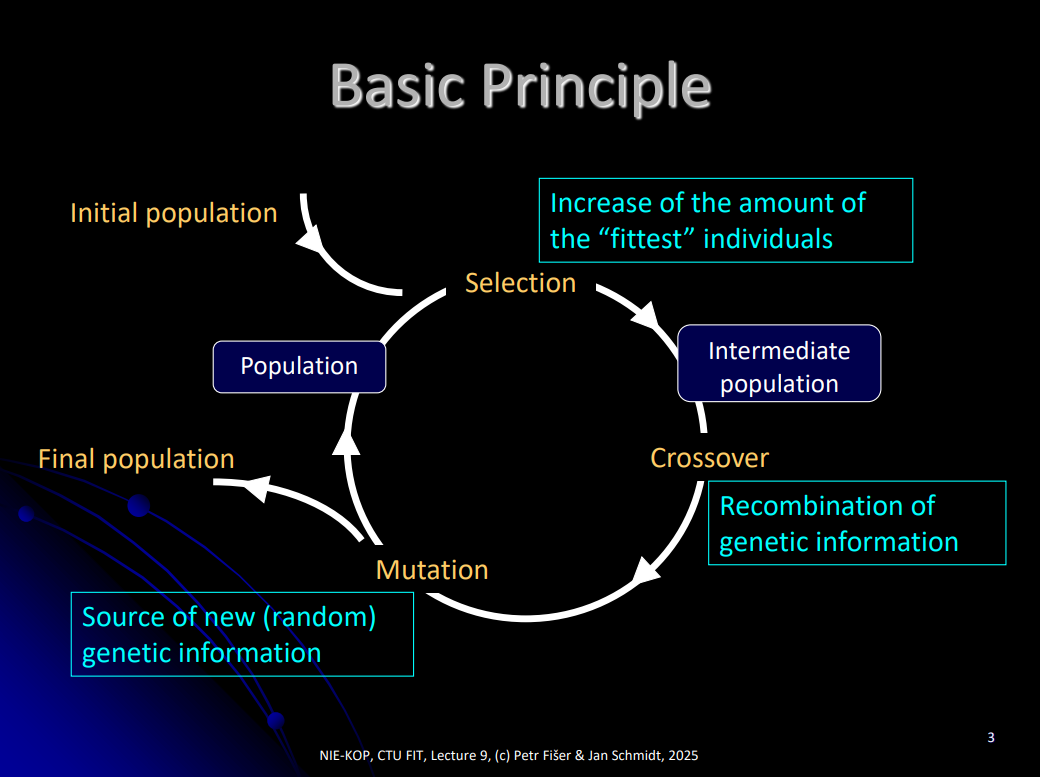
First part: choose the initial population

• first part is constructive (to create the initial population)
  • could be constructed randomly or using some constructive method (but random construction is heavily preferred)
• the population size is usually kept the same through the algorithm run

Repeat: selection → crossover, mutation → replace old generation

Fitness function

• at the beginning of the loop, the fitness of each individual has to be evaluated (to perform the selection)
  • fitness function is essentially the cost function
    • it measures how the given individual is good/bad relative to the whole population
    • it has to be calculated for each individual in the current generation
      • and then again for the next generation and then again
    • it has to be fast (if this is not possible, the genetic algorithm is not the good fit for the problem I am trying to solve)
      • the fitness function complexity should be the first thing to consider when considering genetics algorithms
    • difference between fitness function and cost function
      • fitness function measures the cost of an individual (in the current generation) RELATIVE to the average of the current generation

Selection function

• the input to selection is the fitness information about each individual in the current generation
• the primary aim of the selection is to balance intensification and diversification
  • selection controls this trade-off
• what is selection pressure?
  • it is a probability $p$ of selecting the best individual (with fitness $f_{max}$)
  • every individual $i$ has a probability of being selected
    • where $f_i$ is the (relative) fitness of $i$-th individual, $N$ is the population size
    • the formula depends on the selection method (below)
  • selection pressure is a property/parameter of the selection strategy that we can control to influence GA behavior
    • if the selection pressure is high - results into intensification, converging quickly to the current optimum
      • degereration of a population (small diversity, only a small amount of the best individuals are selected and the next generations will likely be copies/combinations of them)
      • extreme case: $p=1$ means that only the best individual survives
    • if the selection pressure is low - results into diversification, the GA converges to the solution slowly, but it has better exploration
      • if the selection pressure is $p=\frac{1}{N}$, which is the minimal usable selection pressure, all individuals have the same chance of being selected, the information about fitness is not used and GA basically performs a RandomWalk

Selection strategies

• roulette wheel
  • the size of an individual’s section on the roulette is proportional to it’s fittness
    • individuals with bigger fitness have bigger sections and therefore have the bigger chance of being selected
  • the selection is random and the individuals may repeat
  • the result is the intermediate population
    • a population between selection and crossover/mutation (“between generations”)
    • the wheel runs $N$ times, so the intermediate population is of the same size as the previous generation
      • but more fit individuals could appear more often and the worst individuals could not be selected at all
• roulette wheel - universal stochastic sampling
  • the roulette is formed the same way as before
  • then a random angle is marked and this angle divides the roulette into $N$ equivalently distant sections
    • distance is $\frac{2\pi }{N}$
    • the individuals, which are “crossed” with this section are selected
    • so again, if the individual has a big section, it has a higher probability of being selected
  • DISADVANTAGES OF ROULETTE
    • if fitness values of individuals are similar, the roulette has almost no effect (random selection)
    • if one individual is significantly more fit than others, it has a great chance of being selected and the worse individuals have almost no chance
      • leading to early intensification and ending up in some local optimum
  • SOLUTIONS
    • linear scaling
      • the fitness values are linearly scaled to some defined range
        • e.g. rescaling between minimum and maximum values of the fitness functions
      • too fit individuals are not that preferred
      • too weak individuals have higher chance
    • ranking
      • all individuals are ranked by their fitness
      • the relative differences and absolute values are lost, only the order (the rank) of individuals is respected
• tournament selection
  • we randomly select $k$ individuals and they will “compete” against each other and the winner “continues” to the next generation
    • this tournament will be held $N$-times to create a new intermediate generation of the same size
  • we can adjust the selection pressure with the variable $k$
    • with $k=1$, the selection is random (there is no selection)
      • one individual will be randomly selected and it will always win
    • if the $k$ is equal to the size of the current generation ($k=N$), only the best one is continuing into the next generation with no chance for others
• probabilistic tournament
  • the same mechanics as the normal tournament, but the choosing system is different (based on probabilities):
    • there is a parameter $p$:
      • the best individual is selected with probability $p$
      • if not selected, the second best individual is selected with probability $p\ast (1-p)$
      • if not selected, the third one with $p\ast (1-p{)}^2$ etc. until an individual is selected
  • this allows for better selection pressure control (better than just changing $k$ parameter)
• truncation selection
  • we specify a threshold $0<p<1$
    • select the $p\ast N$ fittest individuals
    • copy each selected individual $1/p$ times into the intermediate population
      • each selected individual will have same amount of copies in the next generation (regardless of the real fitness value)
  • common values of $p$: ($p=0.5$ and $p=0.25$)
  • very high pressure, deterministic approach
  • fitness information can be encoded compactly (no real values are needed - all individuals within one category are treated equally):
    • 1-bit fitness:
      • 1 - individual is fit, will advance to next generation
      • 0 - individual is not fit, will no advance to next generation (does not have chance)
    • 2-bit fitness:
      • 11
      • 10
      • 01
      • 00
      • can have different rules for advancing to next generation (e.g. 11 will get 2 copies, 10 will get 1 copy, rest will not advance)

Crossover function

• many different types and approaches, sometimes it is difficult to find the right one for the specific combinatorial problem
• basic idea:
  • usually the properties of two parents are somehow combined to usually produce one or two children (so the children “inherit” parent’s properties)
  • it is a binary operation (two parents are needed)
• types:
  • one-point crossover (for binary encoding)
    • the first child gets first part from the first parent and second part from the second parent (the parts are whole and continuous)
    • the second child gets a second part from the first parent and first part from the second parent
    • the choice of the “line” separating parts in both parents is given randomly
  • two-point crossover (for binary encoding)
    • two positions for a “line” are chosen randomly and the children get a combination of different continuous parts from parents
    • 
  • uniform crossover (for binary encoding)
    • using a bitmask to decide, which parts of the first parent and which parts of the second parent go to which child
      • the bitmask is a random binary vector
      • this crossover is not random at all
        • I cannot introduce new genes (if both parents have 0’s at some position, so they don’t have the “gene”, this crossover operation cannot create it in the child)
        • if both parents have few 1’s, the offsprings will also have a few 1’s
      • the bit-mask is random, yes, but the child’s output is not random, it still inherits the properties from the parents
    • 
  • OX - order crossover (for permutation encoding)
    • the line separating the parts is chosen randomly (could be also two-point way or uniform way)
      • first child gets first part of the parent (as a copy) and the second part is filled up from the second parent using genes, which are not present yet (from the first parent)
        • the filling from the second parent preserves the second parent’s order
    • the already included genes are skipped/excluded
    • 
  • PMX - partially matched crossover
    • 3 ←> 1 is skipped because the 3 is already included in the previous set in the table
      • the same with 6 ←> 8
    • 
    • simply a positional change table is generated from the middle section, which is then applied for both children
  • CX - cycle crossover (for permutation encoding)
    • 
      • first phase: build the cycle
        • my cycle is now empty
        • select the random position (and save it’s value to the cycle)
          • selecting 5
        • look at the same position in the second parent and see, what value is there - find this value back in the first parent
          • looking at 8 in the second parent, finding 8 in the first parent (and saving it into cycle)
        • and it repeats: look at the same position as 8 in the second parent, find it in the first parent and save the value in the cycle
        • after a finite X repeats, we will arrive back at the first value - this is where the cycle generation ends
      • and those values on those positions will “cycle” creating children with different, but inherited properties

Mutation

• mutation randomly changes a gene in an individual
  • it’s an unary operator (only a single individual is modified)
• most important property of mutation operation is that the mutation can introduce new genes
  • which prevents falling into a local optimum and it also diversifies the population
• but warning!
  • more mutations does not mean better solution
  • the mutation rate should be small (up to 5%)
• types:
  • in binary encoding: random flip of one bit
  • in permutation encoding: random exchange of two different positions
  • inversion mutation
    • special type of mutation, it only reorders values in selected part of the representation (it performs the inversion/reversion of the order)
    • it does not introduce new genes, only the positional information is changed

Replacing the old generation

• two ways:
  • the whole population is replaced (“en bloc”)
  • only part of the population is replaced (from both $x$ parents and $y$ children, select $x$ individuals to the new generation)
• techniques:
  • elitism
    • we simply copy the best individuals (no selection, crossover and mutation for them)
      • the “fast track” to the next generation
      • we do not want to accidentally kill them in the process
    • too much elitism is also bad (can cause degeneration of the population)
  • managing the invalid individuals (infeasible states)
    • relaxation (penalize the fitness and they won’t probably be selected in the next round)
    • death (kill them and remove them from population)
    • decoders
      • define crossover and mutation operations in a way, that invalid individuals cannot be made at all
  • population size
    • is usually constant
    • by theory it should grow exponentially with the problem size, but this is often impractical
      • but it should scale with the instance size (but not in the exponential way)
    • if the population size is too small, there is high risk of diversity loss (degeneration of population)

Terminate the loop

• terminate after a fixed number of generations
• or when nothing happens in the last few generations (the changes in the average fitness are small)
  • that means the population is not diverse

Usual parameters

• Population size (typically tens–thousands)
• Crossover rate (typically 80–95 %)
  • this is probability that a randomly selected parents will undergo a crossover to create children
  • if not, the children are exact copies of parents
  • it’s a primary exploration mechanism in GA
• Mutation rate (typically 0.1–5 %)
  • high mutation rate can destroy good individuals, GA also becomes random search
  • low mutation rates do not create enough diversity
• Encoding
• Selection type
• Crossover and mutation type
• Elitism (typically 1-3 individuals)
• Termination condition

Behavior examples in the slides

• slide 61, at the end of the figure, the bad individuals are there because of the mutation
• slide 62, this is essentially a random walk (with remembering the best solutions ⇒ elitism)
  • I can see it on slide 63
• slide 64, we didn’t get to the global optimum

Other evolution-based techniques

Genetic algorithms

• are solving optimization combinatorial problems (in discrete solution spaces)
• encoding: strings (binary strings, strings of integers (permutations))
• using crossover operators, replacing generations etc. - like in this lecture
• usage:
  • when I have discrete choices and I need to explore many combinations efficiently
  • TSP, Knapsack, network design, vehicle routing, timetabling etc.

Genetic programming

• in the 80s there was an idea “how to replace programmers with some evolutionary program”
  • the birth of evolutionary programming
    • the programs, logic circuits, math equations and structures would evolve and get better and better
• encoded in trees
  • internal nodes = operators, functions
  • leaves = variables, constants, terminals
• Genetic programming
• usage:
  • symbolic regression (finding mathematical formulas from data) - an alternative to neural networks
  • trading algorithms, game AI (behavior trees for in-game characters), circuit design, data mining etc.
  • when I don’t know the structure of the solution, just how to evaluate it

Evolutionary programming

• based on evolving and optimizing automatas (e.g. FSM = finite state machine) and their behavior (and state-based systems)
• automatas are fixed in structure, but their parameters are evolving
• encoded as automatas
• operators are only mutations
  • changes of output symbols, transitions, initial states
  • addition/removal of a state
  • crossover would break the automaton’s functionality, mutation preserves the structural integrity
• usage:
  • game AI (NPC behavior), robot control (evolving reactive control systems), pattern recognition etc.

Evolution strategy

• evolving physical objects and find maximums/minimums
  • they have continuous state space (not discrete)
• encoding in the form of vectors of real numbers and their deviations
• done through recombination and mutation
• these strategies have variable parameter values
  • those values can evolve and adapt as well (e.g. the mutation rate)
  • “the evolution learns how to evolve better”
• usage:
  • engineering (shape of the plane wings, car shapes, turbine blade shapes)
  • neural network training, robotics, turing machine optimizations
  • antenna design

---

Tutorial notes

• the cooling coefficient is related to the inner cycle

  • linear change in cooling coefficient there has to be exponential change in the inner cycle count

• the inner cycle count should scale with the instance size

  • for bigger instances there should be bigger inner cycle count
    • and I have to scale the cooling coefficient as well

• bad iterative power = the span of the results is big (each run ends in different value and those values are far from each other)

  • it does not converge well

Genetics

• if I set the mutation too high or too low, the results are getting worse
  • this is good behavior (it’s implemented well)
• the selection pressure is the most important parameter to tune