Metody pro tvorbu indexu v multimediálních databázích (Získávání informací z multimédií), které zásadně zrychlují dotazování. Jsou to obecně datové struktury a metody navžené pro efektivní vyhledávání v databázích, kde je podobnost objektů daná nějakou metrikou (např. euklidovské vzdálenost, edit distance atd.)
- používají se hlavně, pokud neexistuje přirozené pořadí dat, nejdou jednoduše indexovat
- pro obrázky, noty, DNA, audio
Tyto metody jsou založené na předpokladu, že podobnostní funkce (používaná k hledání podobných objektů v multimediální databázi) je metrika - tj. splňuje metrické postuláty:
- je reflexivní - objekt je maximálně podobný sám sobě
- je nezáporná - vzdálenost mezi dvěma objekty je nezáporná
- je symetrická - vzdálenost mezi objekty je “stejná” z obou stran
- má vlastnost trojúhelníkové nerovnosti
Nejdůležitější myšlenkou je využívat trojúhelníkovou nerovnost k filtrování nerelevantních objektů či celých oblastí prostoru, abychom omezili prostor dotazování na skutečně relevantní objekty.
- této technice se říká lower-bounding
- technika, která rychle vyfiltruje nerelevantní výsledky a vrátí přibližné podobné výsledky - je to rychlé a efektivní (oproti drahému počítání vzdáleností mezi všemi objekty) a bez nutnosti počítat exaktní vzdálenosti
- a v té malé vyfiltrované množině už se exaktní vzdálenosti počítají lépe
- k tomu se používají pivoti = určené statické objekty v databázi (slouží jako referenční body pro měření vzdáleností mezi objekty)
- existují různé strategie jejich výběru
Shrnutí
Metrické vzdálenosti mají za úkol minimalizovat množství výpočtu vzdálenosti mezi dvěma objekty → pomocí trojúhelníkové nerovnosti se vytvoří metrický index
- výpočet se pak provádí pouze v pár částech databáze → efektivní vyhledávání
- k indexování se používají pouze vzdálenosti (index nemá tucha o struktuře univerza a často je vzdálenost mezi objekty jediná metrika, kterou index zná))
Další zrychlení provádíme pomocí lower-bound metody, kdy když chceme vypočítat, jestli nějaký objekt je dostatečně blízko k jinému objektu a známe vzdálenost k jinému objektu, u kterého známe vzdálenost k počítanému objektu, tak ho můžeme rychle vyhodit z množiny, protože není dostatečně blízko
- prostě filtrujeme, když vyhledáváme (rychlé vyházení nerelevantních objektů)
- obecný mechanismus pro zrychlení similarity searchu (používám levný lower-bound narozdíl od drahé vzdálenosti)
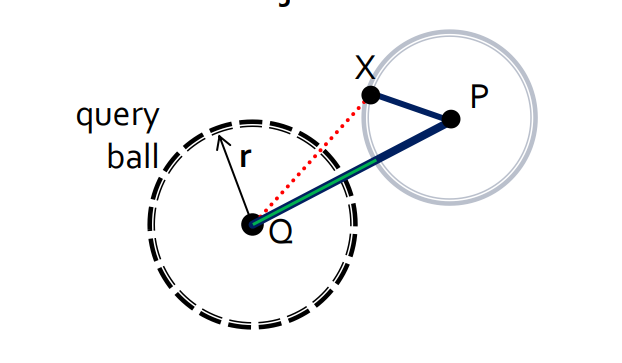
Pivot je statický objekt vybraný z databáze. Jsou předpočítané vzdálenosti mezi objekty k pivotům (ty jsou uložené v metrickém indexu), lze lower-boundovat s pomocí pivotů)
Příklady
Pivotové tabulky
- vyberou se pivoti (referenční objekty)
- předpočítají se vzdálenosti mezi jednotlivými objekty a pivoty v databázi a využívají trojúhelníkovou vzdálenost k eliminaci nepotřebných výpočtů během vyhledávání
AESA
- má předpočítané vzdálenosti mezi všemi dvojicemi
- každý objekt je zastoupen pivotem a tedy máme matici kvadratické velikosti
- drahá konstrukce a O(1) čas hledání nejbližších sousedů
LAESA
- pouze část (k) objektů jsou vybrány jako pivoti - menší matice
- vzdálenosti jsou předpočítané jenom mezi vybranými pivoty
- menší paměťové nároky než AESA
Hierarchické struktury (stromy)
- prostor deskriptorů se rekurzivně dělí do menších a menších oblastí (stromová struktura)
- metrický prostor tedy tvoří hierarchii
- při dotazování se prohledávají pouze ty oblasti (uzly/podstromy), které mají překryv s dotazovacím regionem
- problémy jsou vysoká dimenzionalita dat (tvoření velkých oblastí) a překryvy jednotlivých podstromů, které vedou k pomalejšímu prohledávání více větví
GNAT (Generalized N-ary Tree)
- n-ární strom využívající dělení prostoru/univerza (zobecněnými) nadrovinami
- využívá se lower-bound a pivoti
M-tree
- inspirován R-tree, složené pomocí vložených kulových oblastí a jejich překryvů
- každý uzel ve stromu reprezentuje oblast (kouli) v metrickém prostoru
- využívá se trojúhelníková vzdálenost k efektivnímu vyhledávání
Hashovací indexy
- využívají se hashovací funkce citlivé na lokalitu
- funkce jsou založené na vzdálenostech k vybrané sadě pivotů
- cílem je podobné objekty zahashovat do stejné přihrádky
D-index
- využívá kombinace pivotové tabulky a clusterování
- rozděluje data do clusterů (přihrádek) a využívá jejich vzdáleností k pivotům
Hybridní struktury
- využívají kombinaci více metod a struktur (pro efektivnější a vyváženější filtrování)
PM-tree
- M-tree s globálními pivoty → menší regiony a lepší filtrování
- pivotové tabulky s hierarchickými indexy
M-index
- kombinuje všechny principy MAMs, hybridní struktura
- navíc ukládá informace pro další filtrování
Nějaké databáze ani nemohou mít index (třeba dynamické databáze)
- dynamická databáze - je jako “fronta” např. něco přibývá, něco odtéká (už není relevantní např.)
Indexování je drahá operace (jakože hodně drahá)
- můžu si spočítat, kolik dotazů budu provádět, jestli se mi ten index (výpočetní výkon na něj) vyplatí
- index totiž zrychluje dotazování a zpomaluje operace přidávání, odebírání a aktualizaci dat
- třeba na archivní databáze, kam se moc nekoukám, se mi to moc nevyplatí
Jediný fakt dobrý kritérium, kterýho chci dosáhnout je: DC - Distance computations
- počet výpočtů funkce pro spočítání vzdálenosti
- tuhle funkce chci minimalizovat
Generalizování sahání na disk (I/O operace) - proč je to ošemetné?
- starší disky (magnetický HDD) jsou omezený fyzickýma součástkama (rotování, hlavička hledá místo na disku) - všechno trvalo čas
- sekvenční přístup - projede všechno, jednotlivé přístupy jsou rychlé (jsou za sebou), ale je toho hodně
- když použiju MAM - stromy na lepší indexování - odfiltrování většiny stránek a 1% musím procházet random (je toho méně, ale musím seekovat - to zdržuje)
- 1990 → 2020 se seek moc nezvětšil (fyzikální omezení) + transfer o 2 řády - Mooreovy zákony and all this shit
- SSD - odpadnou mechanické části
- tady už je rychlost vztažená na počet I/Os
Z pohledu interních nákladů? Jak moc se vyplatí implementovat složité MAMs?
Drží se spoustu struktur, počítá se hodně věcí atd. → nároky na infrastrukturu
- třeba Google si drží query requestů, co kdybych se chtěl podívat na další stránku výsledků? Aby to bylo rychlý, ale teoreticky ten query může obsahovat celou databázi (a to pro každého uživatele :O)
Malá vnitřní dimenze = data jsou dobře strukturovaná atd.
Přesnost vs. Rychlost
- např. v relačních databázích chci přesnost
- v similarity searchi přesnost vypadává, a je větší focus na rychlost
- tady měříme precision - jak moc velká je nepřesnost (100% nemůže být)
- zde je větší gain v tom, že trochu zvýšíme nepřesnost, ale na oplátku mega zrychlíme rychlost (v určitých případech se mi tenhle gain vyplatí)