Získávání informací z multimédií

Kromě podobnosti textů a documentů je potřeba také hledat podobnosti v různých typech multimédií (obrázky, audio, video), v podstatě jakkýkoliv nestrukturovaný obsah (také data ze senzorů, grafy, modely atd.). → zabýváme se vyhledáváním v nestrukturovaných datech

Rozdíl mezi reprezentací a vizualizací dat

• záleží jestli je to pro algoritmus (reprezentace) nebo pro člověka (vizualizace)
• v neuronových sítích tohle rozdělení zmizelo
• u spousty věcí je to podobné či skoro stejné

Dva hlavní přístupy k vyhledávání multimédií

Podle kontextu

• popis, anotace, podobnost kontextu
• vysoká sémantika, používají se keywords a tagy, full-text, URL, kategorie
  • většinou anotované lidmi (ale něco jde anotovat automaticky - lokace, čas, URL, GPS souřadnice…)
• kontext sociálních sítí, webových stránek…kde se multimédia nachází
• výhodou je možnost používat vysokoúrovňové dotazy, snadná implementace indexu
• nevýhodou je pracnost, pokud anotují lidé (a také jejich subjektivita - např. u klíčových slov)
• pokud mají textové anotace, je možné je vyhledávat pomocí text-based search (ale je nutné, aby to někdo fakt procházel a anotoval - pokud chybí, je potřeba vyhledávat Podle obsahu

Podle obsahu

• podle skutečného obsahu - raw obsah jako pixely, barvy, zvukové vlny apod.
• většinou jde o nestrukturovaná data, multimediální databáze mají volnou strukturu
• používám, když neexistuje kontext či anotace (nebo se tato vyhledávání vzájemně doplňují)
• složitější - je potřeba vhodně interpretovat volnou strukturu a sémantiku daného multimédia
  • zavádí se různé modely podobnostního vyhledávání

Podobnostní vyhledávání podle obsahu

1. nejdříve je potřeba provést feature extraction - definice a vytahání strukturovaných deskriptorů z média - máme tedy strukturovanou databázi (ale struktura deskriptorů je uživateli schovaná)
   • cílem je z média vytáhnout stručné, definované deskriptory s vysokoúrovňovou informací
2. poté nastupuje Podobnostní funkce pro multimédia - která podle těchto deskriptorů jednotlivé objekty srovná (počítá se vzdálenost mezi jednotlivými objekty)

Deskriptory

• Anotace - externí popisování (vysoká sémantika)
  • explicitní: klíčová slova, full text, URL, klasifikace, GPS
  • contextové: provázání na sociálních sítích, počty likes, komentářů, sdílení atd.
• Content-based deskriptory
  • informace vytažené z vizuálního kontextu (pixely atd.)
    • často nám taková informace dá pouze lokální, omezenou informaci - deskriptory se často kombinují do sebe, abychom dostali informačně zajímavější deskriptor
  • bez deep learningu nejsou tak přínosné
  • standard MPEG7 definuje deskriptory pro obraz, zvuk a pohyb
  • jejich struktura je různá, např: vektor (pro histogramy), množina (vlastnosti), uspořádaná množina (pro časové řady, sekvence, stringy)

Podobnostní funkce pro multimédia

• využívá definované deskriptory a jejich struktury k odhalení podobností mezi jednotlivými multimédii
• zde hodně záleží na struktuře deskriptorů a na sémantice low-level features
• často se používá metrika vzdálenosti - podle které se počítá podobnost mezi multimédii

Příklady podobnostních funkcí

Vektorové vzdálenosti:

• Minkovského vzdálenosti
  • způsob měření vzdáleností mezi vektory - berou se v potaz i nezávislé dimenze
  • složitost $O(n)$
• Cosinové vzdálenosti (záleží na úhlu)
• Kvadratická forma (histogramy)

Adaptivní vzdálenosti:

• EMD - Earth Mover’s Distance ($O(2^n)$ )
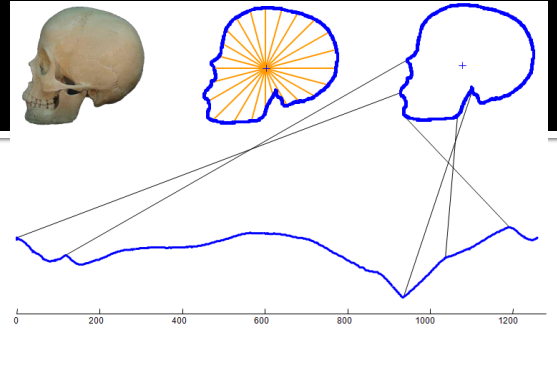
• Hausdorffova vzdálenost
  • pro otisky prstů, mám body pro každý otisk prstu a až budu zjišťovat, který k sobě patří, tak tyto body dám k sobě a pro každý bod najdu nejbližší bod druhého otisku prstu
  • a najdu z nic tu nejdelší vzdálenost a ta určuje, jestli jsou stejné
  • pro podobnost elementů množin se používá tzv. ground distance

Sekvenční vzdálenosti:

• editační vzdálenost
• time warping distance (pro časové řady)
  • např. časovou řadou můžeme popsat nějaký polynom:

Globální features - MPEG7

• histogram použitých barev (RGB)
• struktura barev
• používají se Minkovského vzdálenosti

Lokální features - SIFT nebo SURF

• lokální body, zajímavé body, detekce klíčových bodů v obrázcích
• díky nalezení bodů, které jsou invariantní ke změnám měřítka, rotace a osvětlení můžeme obrázky párovat
• používá se: kvadratická forma, Hausdorffova vzdálenost či Minkovského vzdálenost

Dotazování nad multimédii

• často se používají dotazy typu query-by-example
  • uživatel poskytne nějaký vzorový multimediální objekt (např. obrázek), z tohoto objektu se extrahují jeho deskriptory, které se pak podle podobnostní funkce porovnají s ostatními deskriptory objektů v databázi
  • výsledkem je uspořádaný seznam objektů podle podobnosti jejich deskriptorů

Typy dotazů

• Range Query - vrátí všechny objekty v databází, jejichž vzdálenost od dotazu je menší než určitá vzdálenost
  • je dobré, když dotazující zná sémantiku modelu a umí si určit dobrý threshold
• $k$ Nearest Neighbors (kNN Query) - vrátí se $k$ nejbližších objektů z databáze
  • nejčastější; hlavně v případě, kdy uživatel neznám sémantiku modelu a neumí dobře zvolit práh
• $k$ Reverse Nearest Neighbors (kRNN Query) - vrátí všechny objekty pro které platí, že zadaný objekt je v jejich $k$NN
  • zjistí, jaké všechny objekty ho “mají v sousedství”
  • například se používá v GIS (geografické systémy) pro plánování umístění nových antén

Operátory podobnosti

• operátor je nějaká operace na databázi, která má nějaký výsledek
• dotazy (queries) se od operátorů liší tím, že jsou parametrizované (mají např. zadaný nějaký vzorový objekt) a většinou vrací malou množinu jako výsledek
  • operátory je možné použít vícekrát a mohou vracet velké množiny výsledků
  • operátory nemají parametry
• příklady:
  • Similarity join - spojují deskriptory ze dvou databází na základě nějaké podobnostní funkce
    • pokud se provede na té stejné databázi, tak se jedná o Similarity self-join a hodí se pro detekci duplicitních objektů
  • k Closest Pairs - vybírá dvojice deskriptorů ze dvou databází, které jsou si nejblíže
    • vhodné pro dynamické/streamované databáze, kde je potřeba udržovat nejbližší dvojice

Vícemodální vyhledávání a agregační operátory

• často je potřeba vyhledávát pomocí více modalit (např. klíčová slova + obrázek, či obraz + audio + další relační data)
• aby takový dotaz mohl být zpracován, je potřeba vícemodální informace poskládat dohromady (fúze)

Včasná fúze (early fusion)

• všechny modality jsou agregovány do jediného modelu podobnosti
  • výsledkem je tedy jediný deskriptor pro každý objekt
• příklad: multi-metrický přístup, kde je jeden “velký” deskriptor složen s více subdeskritorů (reprezentující jednotlivé modality) a u každého z nich můžeme určit váhu (“jak moc jsou důležité”)

Pozdní fúze (late fusion)

• používá se, když je složité agregovat všechny modality do jednoho deskriptoru
• každá modalita je reprezentována a dotazována samostatně (máme více podobnostních modelů)
  • vyhledá se podle každé modality a na konci se výsledky zagregují do sebe → k tomu se používají speciální agregační operátory
• Skyline operator (neboli Paretovo optimum)
  • v databázi jsou jednotlivé objekty popsány pomocí více domén či atributů (protože podporujeme více modalit)
  • cílem Skyline operátoru je vrátit takové objekty, které nejsou dominované žádným jiným prvkem (to znamená, že neexistuje žádný jiný objekt, který by byl lepší než aktuální výběr ve všech atributech)
  • hledá vlastně “kompromisy” mezi zadanými modalitami
  • pokud tyto výsledky na grafu spojíme, tak to vypadá jako skyline nějakého města
• Top-k operator
  • každá modalita je zpracována zvlášť podle příslušných modelů → které mi vytvoří seřazení podle dané modality
    • např. mám webové stránky a ty mám seřazené podle podobnosti textů a pak podle podobnosti obrázků, které se tam nachází
  • Top-k operator pak definuje nějakou agregační funkci (např. max(), min(), avg() atd.), kterou zagreguje jednotlivé výsledky příslušných podobnostních funkcí pro jednotlivé modality
  • souvisí také s technikou re-rankování
    • kdy se nejdřív výsledky seřadí podle nějakého parametru, pak druhotně podle jiného parametru apod.

Indexování podobnosti (similarity indexing)

• často je sekvenční procházení velké databáze deskriptorů pomalé (aka porovnávání deskriptoru s deskriptorem), tak se využívají speciální indexy
• cílem indexu je: minimalizovat počet skutečných výpočtů vzdálenosti a I/O operace na disku
• náklady na vytvoření indexu jsou v budoucnosti amortizovány sníženými náklady na dotazování
• pro indexování je důležité mít dobrou distribuci dat v prostoru
  • pokud jsou data dobře distribuovaná, tak je jde dobře rozdělovat do rozlišitelných tříd a indexy fungují dobře
  • pokud jsou data špatně strukturovaná a mají vysokou dimenzionalitu (např. tam, kde jsou data od sebe stejně vzdálená), tak se výhody indexování moc neprojeví a je potřeba využít jiné přístupy → Aproximativní vyhledávání
• v multimediálních databázích se používá hlavně metrické indexování
  • které strukturuje databázi (deskriptorů) pouze na základě vzdáleností (metriky) - skutečné rozměry prostoru mohou být neznámé
  • indexování využívá hlavně vlastnost trojúhelníkové nerovnosti a pivotů k rozdělení a prořezávání metrického prostoru (a tím rychle vyfiltruje nerelevantní výsledky k dotazu)
• MAMs - metric access methods - různé přístupy k tvoření indexů k jednotlivým metrikám

Aproximativní vyhledávání

• cílem je vyměnit přesnost nalezených výsledků za rychlost
• výsledky aproximativních metod se liší podle definovaných záruk:
  • záruka hranice - každý výsledek je do specifikované míry relevantní
  • pravděpodobnostní odhady - s určitou pravděpodobností je daný objekt ve výsledku relevantní
    • takže v průměru je to určité procento výsledků relevantních, zbytek je chybný
  • bez záruky - toto je nejslabší záruka
    • založeno pouze na experimentálním pozorování a vzorkování
• aproximativní vyhledávání upravuje jednotlivé MAMs - metric access methods tak, aby byly ty struktury aproximované, ne tak přesné a aby bylo vyhledávání rychlejší
  • tyto úpravy zahrnují vynechání zpřesnění v pivotových tabulkách (LAESA)
    • nechá se pouze vyhledání množiny relevantních podle indexu, ale konkrétní vzdálenosti už se nepočítají
    • bez záruky přesnosti
  • nebo použití heuristik (u kNN vyhledávání v M-tree)
  • nebo ukládání permutačních indexů místo konkrétních vzdáleností k pivotům
    • ke každému objektu místo vzdálenosti k jednotlivým pivotům uložím pouze permutaci pivotů v pořadí podle vzdálenosti od objektu
    • ztratím informaci o skutečné vzdálenosti a o rozdílech vzdáleností mezi jednotlivými pivoty
• zkráceně
  • aproximativní metody se snaží snížit počet exaktních výpočtů vzdáleností tak, že
    • spoléhají na levnější aproximaci vzdáleností (např. permutační indexy)
    • předčasně ukončí exaktní algoritmus
    • zúží prohledávaný prostor přijetím určité pravděpodobnostní chyby
      • tedy prohledávám menší prostor (=méně výpočtů), ale může se stát, že mimo tento prostor budou ležet ještě nějaké další relevantní výsledky