EDSM - 5. lecture - C1

Systems and Control Theory

Terminology

• signal = a physical quantity evolving in time, it’s a function of time
• system = a change/transformation of a signal from x(t) to another signal y(t)
  • these transformation could be:
    • purposefully designed
      • we want to transform the signal somehow (amplifier, noise filter etc.)
    • unwanted (but unavoidable)
      • e.g. communication - if we send a signal over a long distance, we want it unchanged, but it changes a bit (and we want to study the change to mitigate it)
      • e.g. sensors - studying, if e.g. light trasformed to electrical voltage has some side effects, unwanted transformations etc.

Reference signals

• a system has some behavior and we use a known, well-defined “reference signals” to see, how the system responds
  • they are used as benchmarks to evaluate system’s behavior, compare systems etc.
• if I know these responses, I can then predict the response of the system to more complex inputs

Impulse response

• input is an impulse = an infinitely short spike with finite area (a value for short amount of time and then nothing)
  • like hitting the system with a sharp tap and see, how it reacts
• we measure/study: delay, longevity and oscillation

Step response

• input is an step function = jumps from 0 to some constant value and stays there
  • reveals, how the system responds to a sudden sustained change
  • we measure/study: delay, rise time, overshoot, settling time, steady-state behavior (and steady state error)

LTI = linear time-invariant systems

• systems with two main properties:
  • linearity - if I scale the input, the output will be proportionally scaled as well
    • if I get $y_1(t)$ from $x_1(t)$ and $y_2(t)$ from $x_2(t)$, then I get $y_1(t)+y_2(t)$ for input $x_1(t)+x_2(t)$
  • time invariance
    • if I delay the input, the output will be delayed by the same amount
    • the system’s behavior does not change over time
• the output signal of the system is equal to the convolution (“combination”) of the input signal with the impulse reponse
  • so the impulse function characterizes the LTI system (because it is combined with the input signal) - the impulse response fully describes the way how the system behaves
    • any system could be decomposed into serie of impulses at different times and different strenghts
  • two types of convolution:
    • discrete - uses summation over all input signals (all “impulses”)
    • continuous time - uses integral (time is continuous) to convolute (combine the impulses)

My

• The convolution is the process of breaking any signal into a sequence of impulses (discrete or continuous) of different strenghts and delays. Each impulse produces a system reaction (= impulse response), which is scaled by the impulse strenght and shifted by the impulse delay. The final output is the sum of all scaled and shifted impulse responses (sum or integral - depending of the discrete/continuous domain).

What’s so special about sinusoids?

• sinus function is an eigenfunction to a LTI system
  • if I input a sinusoid, I get also a sinusoid with the same frequency, but it could by scaled and shifted
  • this is possible thanks to mathematical properties of the LTI system
• Fourier’s Theorem = any function could be represented as a sum of sinusoids
• Fourier Series = a discrete sum of sinus functions
  • each periodic function could be decomposed into sinus functions
• Fourier Transformation = the extension to non-periodic functions
  • all functions can be expressed as an integral of sinus functions
  • the transformation decomposes a function into a continuous sum (integral) of sinusoids
  • this is the way how to describe and analyze dynamic systems
    • but it does not tell us HOW to control the system to keep it in steady state - so we use Control theory for it
• and finally, the transformation of the sum of sinus functions is the sum of the transformations of the individual sinus functions (the linear property of the LTI system)
  • different phrasing: The response to a sum of sinusoids (which could represent any complex signal) is the sum of responses to individual sinusoids (thanks to linearity of LTI systems) - which are easy to model and evaluate. This makes Fourier analysis powerful for LTI systems.

Nature limitations

• if I input very high-frequency signals, the system cannot follow perfectly, there are delays etc. because of nature physics (atoms cannot move faster)

Control theory

• is about controlling the systems, we have some desired output (then some actual outputs) and we try to reach the desired output
  • the systems are dynamic and we are dealing with them in time
    • why? because the signals are physical quantities that can change over time, and systems are just transformations of these signals, which produce some outputs
    • some outputs are unavoidable and unwanted, so we have to control them to minimalize them
• 
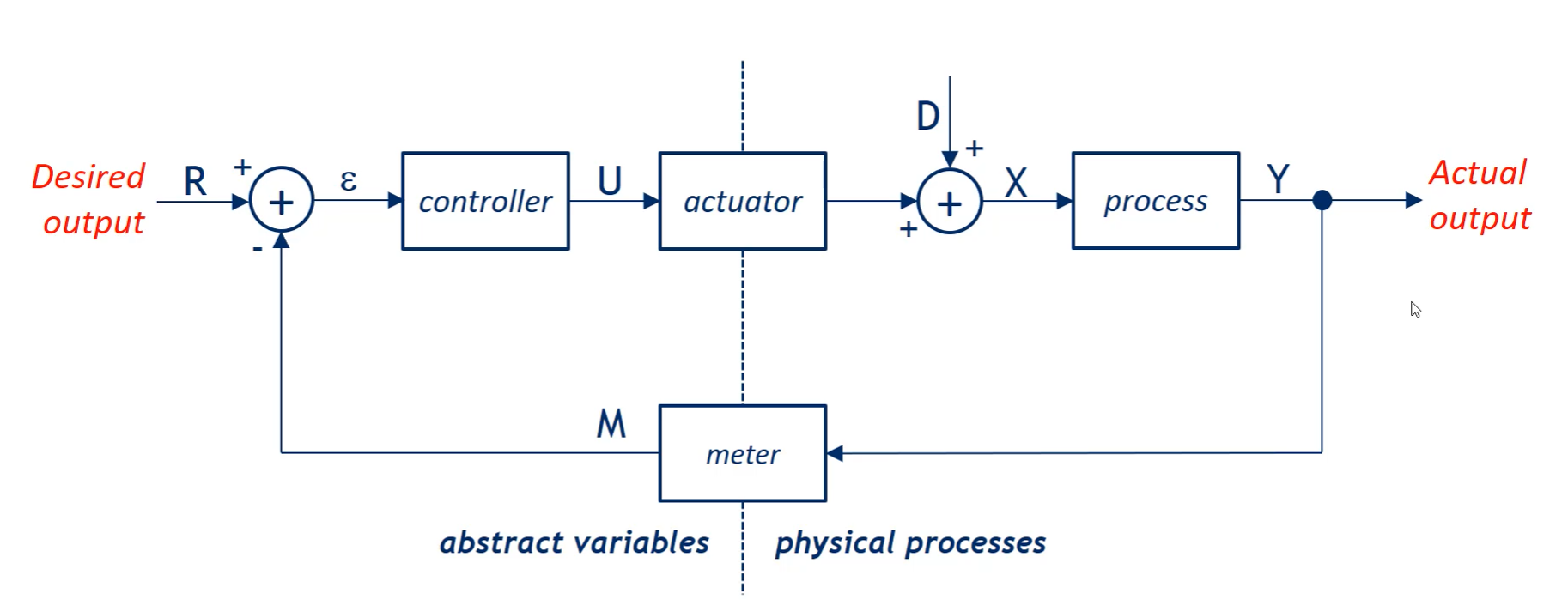
  • this is done with a “negative feedback” as the difference
    • the controller has to adjust the system in the opposite direction of the deviation to maintain the dynamic stability
    • examples:
      • so in terms of heating, when the desired output is 20°C and actual output is 15°C, the difference is -5°C → we need to add +5°C and vice versa
      • if the car drifts to the right, we have to steer to the left
  • meter measures the actual output with sensors and translates the inputs into electrical or digital information (provides the feedback about the current state)
    • it does not have to be capable of measuring all the real outputs (measurement limitations) and there could be delays in measuring
  • controller steers the behavior of the system based on the desired output and the actual output (that is why the system is dynamic) by creating action $U$
    • the deviation is called a steady state error and it should be minimized by the controller
    • we don’t want the change to be too slow (poor performance, causing delays) or too quick (risk of high oscillations, overshoot and system instability etc.)
      • the corrections should not be too slow or too fast
    • the purpose of the controller is to realize an overall dynamic behavior of the system (while maintaining speed vs. stability) with respect to how all parts of the system react to inputs and how they adjust over time
      • this is the essence of the Dynamic Systems Control
  • actuator transforms the information about action $U$ from the controller to physical action to change the system’s behavior
    • e.g. motor, valve, heater etc.
    • it can also have external effects on entirely different systems (not related to the process)
  • process is the physical system that is being controlled itself, it captures the actual change of the behavior, it can have external side effects = disturbances
  • there could be delays in all parts of the diagram
  • steady state = there is an alignment between desired and actual state
• problems
  • when we don’t have negative feedback (the system runs blindly without corrections)
    • e.g. microwave timer (does not take into account whether the food is hot or not)
  • when we have positive feedback
    • “when a car is drifting to the left, so we steer more to the left”
    • “when a country battles inflation, so we print more money”
    • “nuclear chain reaction without control”
    • small errors are not corrected (the “opposite way”), but amplified and system becomes unstable

Application in engineering

• we develop/invent new systems and we need to know, how the system reacts to external inputs and how do we control and correct the system to be stable
  • done by systems of differential (continuous) or difference (discrete) equations (involving the negative feedback)
• a system is dynamically stable iff a bounded input results in a bounded output